Filtracja
Aby poprawić percepcję zmian patologicznych w
obrazach mammograficznych stosuje się filtrację falkową z dwuwymiarowym jądrem
przekształcenia. Algorytm ten można podzielić na 7 faz:
1.
transformacja obrazu do postaci heksagonalnej
2. podział na 4
podpasma
3. predykcja w trzech podpasmach (ang. prediction)
4. dookreślanie pasma niskoczęstotliwościowego (ang. update)
5.
modyfikacja współczynników transformaty
6. odtworzenie sygnału do
postaci heksagonalnej
7. transformacja z postaci heksagonalnej do
obrazu wynikowego
Faza 1 i podobnie faza 7 są względem siebie operacjami
komplementarnymi. Transformacja obrazu do postaci heksagonalnej została
zrealizowana w taki sposób, że co drugi rząd jest niejako przesuwany o 1/2
piksela, a nowe piksele są obliczane na podstawie punktów, które znajdowały się
w najbliższym sąsiedztwie obliczanego punktu w danej linii (średnia arytmetyczna
punktów przed- i za- obliczanym punktem). Faza 7 realizowana jest w podobny
sposób – w co drugim rzędzie punkty przesuwane są na swoje miejsca i ponownie
obliczane na podstawie wartości punktów sąsiednich. Przekształcenie to nie jest
oczywiście w 100% odwracalne i powoduje wygładzenie obrazu (filtrację
dolnoprzepustową), jednak korzyści płynące z lepszego dopasowania jądra
przekształcenia w dalszym procesie filtracji (w stosunku do tradycyjnej
transformaty falkowej) rekompensują tą niedogodność.
Faza 2 polega na
podziale punktów obrazu na 4 grupy, które po fazie predykcji i dookreślania
zostaną przekształcone w 4 podpasma (patrz rys. 1):
* niskoczęstotliwościowe (a)
* wysokoczęstotliwościowe zorientowane na zmiany występujące w obrazie na osi pochylonej o kąt 0 stopni (c0)
* wysokoczęstotliwościowe zorientowane na zmiany występujące w obrazie na osi pochylonej o kąt 60 stopni (c60)
* wysokoczęstotliwościowe zorientowane na zmiany występujące w obrazie na osi pochylonej o kąt 120 stopni (c120)
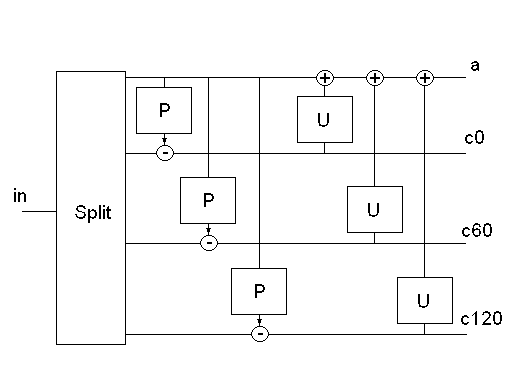
Rys. 1 Schemat liftingu w transformacie heksagonalnej
Proces predykcji (faza 3)
realizowany jest w taki sposób, że na podstawie wybranych punktów z pasma
bazowego przewidywane są odpowiednie punkty pozostałych pasm, a następnie
przewidziane wartości są odejmowane od wartości oryginalnych. Filtr predykcji
powinien być dobrze dopasowany do charakterystyki istotnych diagnostycznie
obiektów w obrazie (np. mikrozwapnień). Przyjmuje się, że znajdując się w
centralnym punkcie mikrozwapnienia o charakterystyce zbliżonej do dwuwymiarowej
funkcji Gaussa próbujemy przewidzieć ten punkt na podstawie najbliższego
sąsiedztwa z pasma bazowego. Mając dobrze dopasowane jądro przekształcenia w
wyniku filtracji uzyskamy największe wartości współczynników w obszarach
najlepiej dopasowanych do charakterystyki filtru, czyli przyjętego modelu
obiektów użytecznych. Daje to informacje w pasmach wysokoczęstotliwościowych o
szczegółach i wskazuje na potencjalne miejsca występowania wzorców istotnych
diagnostycznie. Dane o szczegółach są następnie użyte do modyfikacji wartości w
paśmie niskoczęstotliwościowym (chodzi o zachowanie składowej stałej) w wyniku
operacji dookreślania. W niniejszym projekcie zastosowano trzy bloki predykcyjne
dla poszczególnych kanałów wysokoczęstotliwościowych (c0, c60 i c120).
Współczynniki predykcji wynosiły odpowiednio 1 /2, 1/8 i –1/16 (model 1) oraz 1
/2, 1/10 i –5/100 (model 2). Współczynniki w procesie dookreślenia wynosiły 1/8
dla obydwu modeli. Na rys.2 przedstawiono wartości współczynników predykcji
(model 1) dla poszczególnych kanałów.
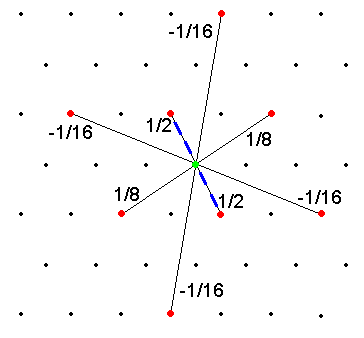
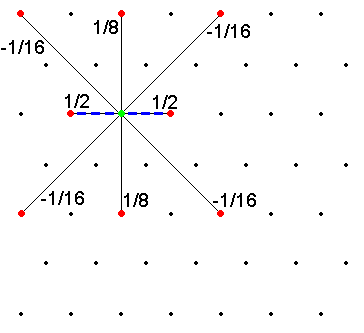
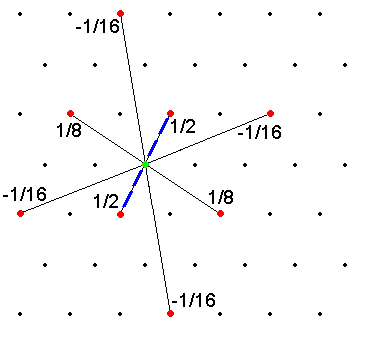
Rys. 2 Rozkład współczynników predykcji dla kanałów: c0, c60 i c120
Zastosowano adaptacyjną metodę modyfikacji wartości współczynników
transformaty. Sprawdzane jest otoczenie badanego punktu (w kanałach
wysokoczęstotliwościowych). Jeżeli średnia z wartości bezwzględnych otoczenia
jest mniejsza od wartości bezwzględnej badanego punktu, to wartość tego punktu
jest zwiększana o 30% (A=1.3), dla pozostałych przypadków wartość nie jest
zmieniana (dla B=1) zgodnie ze wzorem:
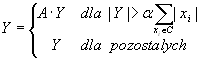 (1)
(1)
gdzie Y –
współczynnik falkowy, C –kontekst jak na rys. 5, xi – współczynniki kontekstu, A
dobierana waga wzmocnienia, α - zależne od skali i położenia uwydatnienia
obiektu.
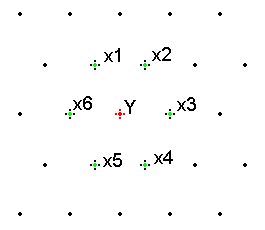
Rys. 3 Sąsiedztwo modyfikowanego współczynnika
transformaty, określone jako C we wzorze (1).




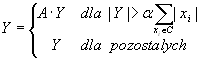 (1)
(1)
